Combinatorics

Permutations

Permutations represent the number of different possible ways we can arrange a number of elements.

Example: 3 racers finish a race. How many ways can the three racers finish? We use a factorial to determine this:

\[ 3!= 3 * 2 * 1 = 6 \]

Therefore, there are six permutations for this three-person race.

Solving Variations with Repeating Values

Variations – the total number of ways we can pick and arrange some elements of a given set.

\[ \overline V_p^n = n^p\]

n = the total number of elements we have available

p = the number of positions we need to fill

Note: Variations do not take into account double counting elements, as can be seen in the dice example below.

Example 1: the number of combinations when rolling two 6-sided dice is 62 = 36 variations.

Example 2: the number of combinations on a set of briefcase locks (six dials with 10 digits on each dial) is 106 = 1,000,000 variations.

Solving Variations without Repeating Values

The number of variations without repetition when arranging ‘p’ elements out of a total of ‘n’.

\[ {V_p^n} = \frac{n!}{(n-p)!}\]

Example 1: We have a team of five runners and need to pick four of them for a relay. Here p = 4, and n = 5.

\[ {V_4^5} = \frac{5!}{(5-4)!} = 120\]

Example 2: Picking a 4-person relay from a team of 20 people:

\[ \frac{n!}{(n-p)!} = \frac{20!}{(20-4)!} = \frac{20!}{(16)!} = 17*18*19*20 = 116,280\]

Solving Combinations

Combinations – the number of different ways we can pick certain elements of a set.

\[ C_p^n = \frac{V_p^n }{P_p} = \frac{n!}{p!(n-p)!}\]

n = the total number of elements we have available

p = the number of positions we need to fill

Example: You have 10 employees and need to pick a team of 3 employees for a project. How many Combinations are there?

\[ \frac{n!}{p!(n-p)!} = \frac{10!}{3!*7!} = \frac{8*9*10}{1*2*3} = 120 \]

Symmetry of Combinations

Example: Choosing 3 employees to put on a team is the same as picking 7 employees to leave off of the team.

SymmetryExplainedDownload

Solving Combinations with Separate Sample Spaces

Sometimes a Combination can be a mixture of different smaller events. Calculating the total number of combinations is by multiplying the number of options available for each individual event.

Example 1: A lunch special consists of a sandwich, side, and drink. There are 3 sandwiches, 2 sides, and 2 drinks available. How many combinations of this lunch are there?

\[ 3 * 2 * 2 = 12\]

Example 2: An online consists of a heading (3), thumbnail (5), post description (3), and button(2). How many ad combinations are there?

\[ 3 * 5 * 3 * 2 = 90\]

It can take a lot of time and resources to test 90 ads. Removing several options will greatly decrease the time and resources needed to test these ads. This is often done in the real world.

Combinatorics in Real-Life: The Lottery

Pick 5 numbers between 1 and 69, and a Powerball between 1 and 26.

These are two separate events. Remember that the likelihood of two independent events occurring simultaneously equals the product of their individual probabilities. First we need to determine the probability of guessing the Powerball, and guessing the correct 5 numbers.

\[ P(Powerball) = \frac{1}{26}\]
\[ C_p^n = \frac{n!}{p!(n-p)!} = \frac{69!}{5!(64)!} = \frac{65*66*67*68*69}{1*2*3*4*5} = 11,238,513\]
\[ P(5 \: numbers) = \frac{1}{11,238,512}\]
\[ P(lottery) = P(Powerball) * P(5 \: numbers) = \frac{1}{26} * \frac{1}{11,238,512} = \frac{1}{292,201,338}\]

Combinatorics Summary

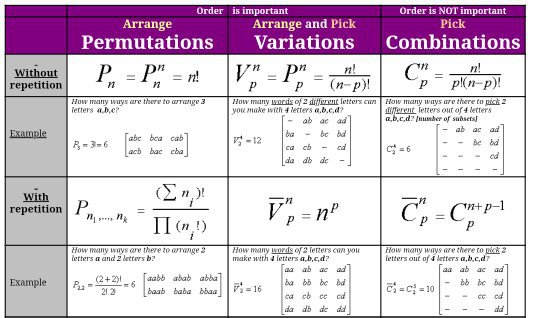
No Repetition

\[P_n = n!\]
\[ {V_p^n} = \frac{n!}{(n-p)!}\]
\[ C_p^n = \frac{n!}{p!(n-p)!}\]

Repetition

\[ \overline V_p^n = n^p\]
\[ \overline C_p^n = \frac{(n+p-1)!}{p!(n-1)!}\]

Symmetry

\[ C_p^n = C_{n-p}^n\]

Combinatorics Cheatsheet

Course-Notes-CombinatoricsDownload