Sets and Events
Set – a collection of elements which hold certain values. Sets are denoted in UPPER CASE text.
Element – Elements are denoted in lower case txt. They make up sets.
Null Set – an empty set or null set. Denoted with a ‘Ø’ symbol.
Non-empty Sets – can be finite or infinite.
Part of a Set
If ‘x’ is an element of the set ‘A’, we notate it like this:
If set ‘A’ contains element ‘x’, we notate it like this:
Element ‘x’ is not in set ‘A’.
Set ‘A’ does not contain ‘x’.
To denote all elements in a set we use the symbol ‘∀‘.
‘∀ x in A’ means ‘all elements of A’ .
Adding a colon (:) means ‘such that’. This is useful when we want to make statements about a specific group of elements within a set.
Example: to select all even elements in an set:
∀ x in A : x is even
subset – A set that is fully contained in another set. Every element in A is also in B. This is written as:
Note that every set A has two subsets: Itself (A), and the null set (Ø).
Ways Sets can Interact
Events can interact in three ways:
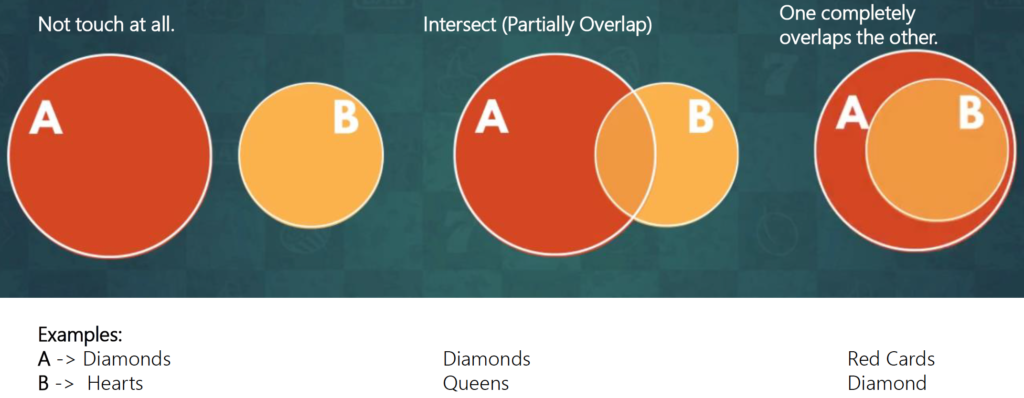
- Not Touch
- These events can never happen simultaneously.
- Event A occurring guarantees that event B is not occurring, and vice versa.
- Intersect
- These events can occur at the same time.
- Overlap
- One event can only occur if the other one does as well.
Intersection of Sets
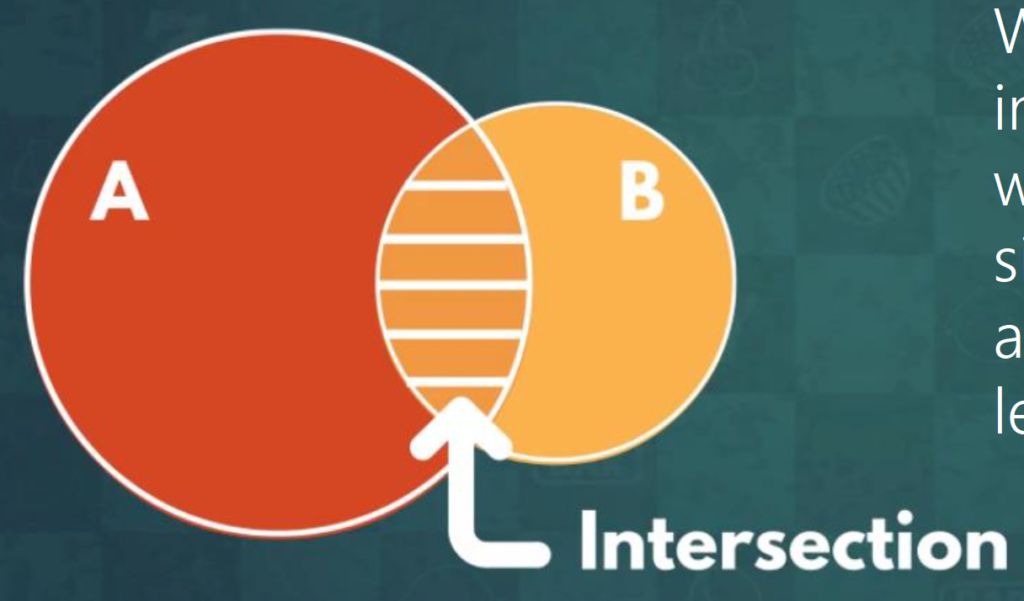
The Intersection of two or more events expresses the set of outcomes that satisfy all the events simultaneously. We use intersections only when we want to denote instances where both events A and B happen simultaneously. Graphically, this is the area where the sets intersect. The intersection is expressed mathematically like this:
When one event is inside another event like this:

We write the intersection equation like this:
Union of Sets

The union of two or more events expresses the set of outcomes that satisfy at least one of the events. Graphically, this is the area that includes both sets. It is expressed mathematically like this:
Three Types of Unions
Sets Do not Touch at All

Sets Intersect

Sets Overlap

Mutually Exclusive Sets

Mutually Exclusive Sets – Sets which are not allowed to have any overlapping elements.
Mutually Exclusive sets have the empty set as their intersection.
If the intersection of any number of sets is the empty set, then they must be mutually exclusive.
Complements of a Set
Sets have complements too.
Complement Set – all values that are part of the sample space, but not part of the set. Note that all complements are always mutually exclusive.
Independent and Dependent Events
Independent Events – Events whose theoretical probability remains unaffected by other events.
Dependent Events – Events whose probabilities vary as conditions change.
Conditional Probability of A Given B
The probability of getting A given that B has occurred is written like this:
Conditional Probability is used to distinguish dependent from independent events.
The Conditional Probability Formula
Conditional Probability – the likelihood of an event occurring, assuming a different one has already happened.
Independent Variables
Two events are independent if:
If any two events are independent, then:
The Law of Total Probability
The Additive Law
The Multiplication Law
Bayes’ Law
Bayes’ Law allows us to find a relationship between the different conditional probabilities of two events.
