Mathematics

What is a Matrix?

• In linear algebra, a matrix is a rectangular array of numbers (or other mathematical objects) arranged in rows and columns. Matrices are used to represent linear transformations between vector spaces, and they play a central role in many areas of mathematics and physics.
• The size of a matrix is given by its dimensions, which are typically written as m × n, where m is the number of rows and n is the number of columns. The individual elements of a matrix are often denoted by a_ij, where i represents the row index and j represents the column index.
• Matrices can be added, subtracted, and multiplied in various ways, and these operations satisfy certain algebraic properties. For example, matrix multiplication is associative (i.e., (AB)C = A(BC)), but it is not in general commutative (i.e., AB ≠ BA).

Scalars and Vectors

• Scalars are like numbers on the number line, with a single value.
• Vectors are a one-dimensional list of scalars. This can be represented by a row or a column in a matrix.
• Matrix – a collection of vectors.

What is a Tensor?

• A 1 x 1 Tensor (Rank 0) is a Scalar.
• An m x 1 Tensor (Rank 1) is a Vector.
• An m x n Tensor (Rank 2) is a Matrix.
• A k x m x n Tensor (Rank 3) is a collection of Matrices.

In code, we often store Tensors in ndarrays.

Addition and Subtraction of Matrices

In linear algebra, addition and subtraction of matrices involve combining two matrices of the same size (i.e., with the same number of rows and columns) by adding or subtracting their corresponding elements.

Formally, if A and B are two m x n matrices, then their sum A + B is an m x n matrix, where the element in row i and column j of A + B is the sum of the elements in row i and column j of A and B. In other words, (A + B)ij = Aij + Bij.

Similarly, the difference A – B of two matrices A and B of the same size is also an m x n matrix, where the element in row i and column j of A – B is the difference between the elements in row i and column j of A and B. In other words, (A – B)ij = Aij – Bij.

Some properties of matrix addition and subtraction include:

• Matrix addition and subtraction are commutative: A + B = B + A and A – B = -(B – A).
• Matrix addition and subtraction are associative: (A + B) + C = A + (B + C) and (A – B) – C = A – (B + C).
• Scalar multiplication distributes over matrix addition and subtraction: k(A + B) = kA + kB and k(A – B) = kA – kB for any scalar k.
• Adding or subtracting a matrix with itself results in a matrix that is twice (or zero times) the original matrix: A + A = 2A and A – A = 0.

Transposing a Matrix

In linear algebra, transposing a matrix involves flipping its rows and columns, so that the element in row i and column j becomes the element in row j and column i. The resulting matrix is called the transpose of the original matrix, and is typically denoted by a superscript “T” or a superscript apostrophe.

More formally, if A is an m x n matrix, then its transpose A^T is an n x m matrix, where the element in row i and column j of A^T is the element in row j and column i of A. In other words, (A^T)_ij = A_ji.

The transpose of a matrix has several useful properties. For example:

• The transpose of a transpose is the original matrix: (A^T)^T = A.
• The transpose of a sum of matrices is the sum of the transposes: (A + B)^T = A^T + B^T.
• The transpose of a product of matrices is the product of the transposes in reverse order: (AB)^T = B^T A^T.

Dot Product

• Multiplied lists need to be the same length.
• The dot product is is the sum of the products of the corresponding elements.
• There are two ways to multiply:
  • Dot Product (Inner Product or Scalar Product)
  • Tensor Product (Outer Product) – will not be used for now.

The Dot Product of Matrices

• We can only multiply an m x n matrix with an n x k matrix. (i.e. the number of columns of the first matrix must equal the number of rows in the second matrix.)
• The dot product of matrices, also known as matrix multiplication, is an operation that combines two matrices to produce a new matrix. Unlike addition or subtraction, matrix multiplication is not commutative, meaning the order of the matrices matters.
• To perform the dot product of matrices, let’s consider two matrices: A with dimensions m × n and B with dimensions n × p. The resulting matrix, denoted as C, will have dimensions m × p.
• When we have a dot product, we always multiply a row vector times a column vector.

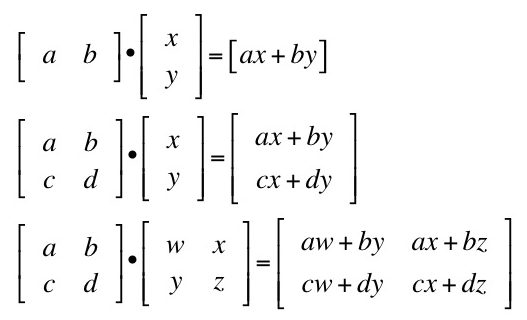
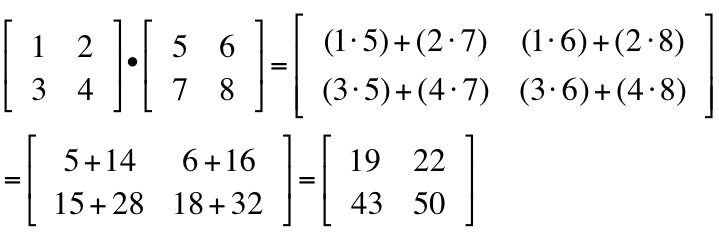
How is Linear Algebra Useful?

Some of the key applications of linear algebra in data science include:

1. Vectorized Code: Array Programming, Numpy.
2. Linear Regression: Linear algebra is fundamental to linear regression, a widely used statistical technique for modeling the relationship between variables. Linear regression involves fitting a linear equation to observed data points, and it relies on concepts such as matrix multiplication, least squares optimization, and matrix inverses.
3. Dimensionality Reduction: Techniques like Principal Component Analysis (PCA) and Singular Value Decomposition (SVD) are used for dimensionality reduction in data science. These methods utilize linear algebra to transform high-dimensional data into a lower-dimensional representation while preserving essential information.
4. Machine Learning: Many machine learning algorithms, such as support vector machines (SVMs), logistic regression, and neural networks, heavily rely on linear algebra. Matrix operations, such as matrix multiplications and dot products, are used for model training, parameter estimation, and prediction tasks.
5. Image and Signal Processing: Linear algebra is extensively used in image and signal processing tasks. Techniques like Fourier Transform, convolution, and wavelet analysis make use of linear algebra operations to analyze and manipulate images and signals.
6. Recommender Systems: Recommender systems, which are used to predict user preferences and make personalized recommendations, often employ linear algebra techniques. Matrix factorization and collaborative filtering methods are used to analyze large user-item matrices and extract latent features.
7. Graph Analysis: Graphs and networks are prevalent in data science applications, such as social network analysis and recommendation systems. Linear algebra methods like eigenvector centrality and graph Laplacian are used to extract important features and understand the structure and connectivity of the graphs.
8. Clustering and Classification: Linear algebra techniques are applied in clustering algorithms such as k-means clustering and spectral clustering. Similarly, linear classifiers like linear support vector machines (SVMs) rely on linear algebra operations to separate data points into different classes.