- Choose the number of clusters.
- Specify the cluster seeds. A seed is basically a starting centroid.
- Assign each point to a centroid according to their Euclidean distance from the seeds.
- Adjust the centroids.
- Were points reassigned? If so, go to step 3. If not, clustering is complete.
Description
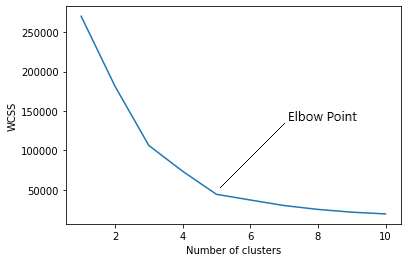
The k-means algorithm requires the user to specify the number of clusters, k, that should be formed, as this parameter affects the final clustering result. One way to determine the optimal value of k is to use the elbow method, which involves plotting the sum of squared distances as a function of k and selecting the value of k where the decrease in the sum of squared distances starts to level off.
K-means clustering is widely used in various fields, such as image segmentation, customer segmentation, and anomaly detection. It is a relatively simple and efficient algorithm that can handle large datasets, but it is sensitive to the initial choice of centroids and can converge to a local minimum rather than the global minimum. Therefore, it is often run multiple times with different initializations to improve the chance of finding the optimal solution.
Within-Cluster Sum of Squares (WCSS)
WCSS (Within-Cluster Sum of Squares) is a metric used to evaluate the quality of a clustering solution. It measures the sum of the squared distances between each data point and its nearest centroid in the same cluster. In other words, WCSS represents the total variation within each cluster.
The WCSS value is commonly used in the elbow method for determining the optimal number of clusters in a k-means clustering algorithm. The elbow method involves plotting the WCSS values against the number of clusters and identifying the “elbow” or bend in the curve where adding more clusters does not significantly reduce the WCSS anymore. The number of clusters corresponding to the elbow point is often chosen as the optimal number of clusters for the given dataset.
Pros and Cons of K-Means Clustering
Pros:
- Simple and easy to implement: K-means is a simple algorithm that is easy to implement, making it a popular choice for clustering problems.
- Fast and scalable: K-means is a relatively fast algorithm that can handle large datasets with many features, making it suitable for high-dimensional data.
- Works well with spherical clusters: K-means assumes that the clusters are spherical and of similar size, and it performs well when this assumption holds true.
- Allows for easy interpretation: K-means provides a clear and intuitive way to interpret the resulting clusters, as each cluster is represented by its centroid and the data points assigned to it.
Cons:
- Sensitive to the initial centroids: K-means clustering is sensitive to the initial choice of centroids, and different initializations can lead to different solutions.
- Assumes equal cluster sizes: K-means assumes that each cluster has an equal number of data points, which may not hold true in practice.
- Limited to numeric data: K-means only works with numeric data and cannot handle categorical or mixed data types.
- May not work well with non-spherical clusters: K-means may not perform well when the clusters are non-spherical or have different shapes and sizes.
- Sensitive to outliers.
- Standardization
Should we Standardize Data with K-Means?
Pros:
- Equalizes the scales: Standardizing data ensures that all features are on the same scale, making it easier to compare the importance of different features in determining the cluster assignments. This is important because K-means clustering is a distance-based algorithm, and features with larger scales may dominate the distance calculations.
- Prevents bias: Standardizing data prevents features with larger scales from dominating the clustering process and potentially introducing bias. This is important because K-means clustering aims to minimize the within-cluster sum of squares (WCSS), and features with larger scales may contribute more to the WCSS calculation.
- Improves convergence: Standardizing data can help the K-means algorithm converge faster and improve the stability of the clustering solution. This is because standardizing data can reduce the range of values that each feature can take, which can help the centroids converge to the optimal values more quickly.
Cons:
- May distort the original data: Standardizing data can distort the original distribution of the data and may remove meaningful information, such as outliers or rare events. This is because standardization transforms the data to have a mean of zero and a standard deviation of one, which may not accurately represent the original data distribution.
- May not be appropriate for all data types: Standardizing data assumes that the data is normally distributed, which may not hold true for all datasets. For example, if the data is highly skewed or has a non-normal distribution, standardization may not be appropriate and may lead to suboptimal clustering solutions.
- May not improve results: Standardizing data does not always improve the quality of the clustering solution, and may even lead to worse results in some cases. This is because standardization may introduce noise or distortions that affect the distance calculations and clustering assignments.
How is Clustering Useful?
- Data exploration: K-means clustering can be used for exploratory data analysis to identify potential patterns or relationships within a dataset. This can be useful for gaining a better understanding of the underlying structure of the data and for identifying potential outliers or anomalies.
- Customer segmentation: K-means clustering can be used to segment customers based on their behavior or preferences. This can be useful for developing targeted marketing campaigns or for identifying areas for improvement in customer service.
- Image compression: K-means clustering can be used for image compression, where the algorithm identifies clusters of similar pixels and replaces them with a single representative pixel. This can help to reduce the storage requirements for digital images without significantly affecting their quality.
- Anomaly detection: K-means clustering can be used for anomaly detection, where the algorithm identifies data points that do not belong to any of the clusters or that belong to a cluster with a significantly different distribution. This can be useful for identifying potential errors or fraud in financial or security applications.
- Feature engineering: K-means clustering can be used for feature engineering, where the clusters can be used as new features in a machine learning model. This can help to improve the accuracy of the model by providing additional information about the relationships between the input variables and the target variable.
